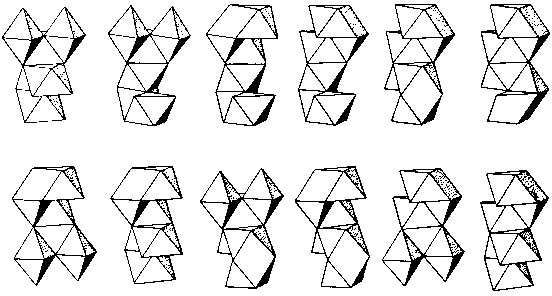
[Home] [Contents][Figures] [Search] [Help]
One of the charms of the simple two-dimensional dissection puzzles shown in Chapter 1 is that they construct many different simple geometrical shapes with the same set of pieces. Some of the polyhedral block puzzles in Chapters 3 and 18 construct multiple shapes but they are non-interlocking. The difficulty of achieving this feature with interlocking puzzles was demonstrated in Chapter 11 by a pair of designs that succeeded only partially. Is it possible for a set of interlocking puzzle pieces to construct many different polyhedral shapes?
Recall the simple two-piece dissection of the rhombic dodecahedron shown in Fig. 147. These half-pieces can be joined in pairs in different ways to form puzzle pieces. Excluding those that are impossible to assemble or have an axis of symmetry, there are 12 such pieces, shown in Fig. 175.
Fig. 175
Let us make a list of possible constructions, i.e. ways that R-D blocks can be clustered symmetrically. To keep things simple, consider only those with six or fewer blocks. Eight such figures are shown in Fig. 176a.
Fig. 176a
Editor's Note: Stewart named this puzzle The Peanut Puzzle.
Fig. 176b
Now for the interesting part. Can you find a subset of six pieces from the set of 12 that will construct all eight of the above figures? Do not be too discouraged if not, because Beeler's computer could not either. Of the 924 possible such subsets, there is one, however, that will construct seven of the eight figures. Find it if you can, keeping in mind that the seeking may be more fun than the actual finding.
Considering the thousands of different possible subsets of puzzle pieces and the many interesting constructions possible with any of them, the recreational potential for this family of puzzles is vast and practically unexplored. Choose your own personal subset of puzzle pieces and compile your own library of geometrical or animated shapes that they will construct (see Fig. 177). The pieces are also great fun just to doodle with. Any closed loop can be considered a solution of sorts.
Fig. 177
A well-crafted set of these pieces makes a most satisfactory puzzle. Each half of each puzzle piece is made of three squat octahedra building blocks joined accurately together, and the full pieces are then made up of these half-pieces joined different ways.
(Incidentally, to digress slightly, a fascinating recreation is to determine how many of the eight constructions shown in Fig. 176 are space-filling. You may be surprised at the answer.)
The Six-Part Invention design leads by analogy to one based on cubes in place of rhombic dodecahedra, dissected the same way. These half-pieces can be joined in pairs eight different ways, as illustrated in Fig. 178.
Fig. 178
The obvious question is whether these eight pieces can be assembled into a cube. That they do, and much more. Here is one of the best examples in this book of a geometrical recreation that lends itself to use in the classroom. For example:
| 1. | Using two disconnected half-pieces, find all the ways that they can be joined face-to-face. You will of course arrive at the set of eight pieces, but this simple exercise can be quite instructive. |
| 2. | Prove that four pieces are the fewest that can be connected together in a closed loop. Prove that the square is the only such possible figure. Can two separate squares be made using all eight pieces? Why not? |
| 3. | Prove that the 2 x 4 rectangle is impossible. (Problems of this sort can always be solved systematically by trying every piece in every possible combination, but look for shorter and more elegant proofs using logic. Now what other shapes cannot be made for the same reason? |
| 4. | Assuming all solutions to be closed loops, prove that an even number of pieces must always be used. Find all possible solutions using six pieces. Likewise using all eight pieces. Examples are shown in Fig. 179a. |
Fig. 179a
Editor's Note: Stewart named this puzzle Pieces of Eight.
Fig. 179b
Six of the pieces have reflexive symmetry and the other two are a reflexive pair. It necessarily follows that every solution must either be self-reflexive or occur in reflexive pairs. (These pairs are not counted as separate solutions.) Can you figure out why?
Some of the most fundamental questions in physics have to do with symmetry, and perhaps this puzzle will stimulate the student's interest in this fascinating subject. If the most elementary particles in the universe and all of the laws governing them were symmetrical (which is not to say they are), would it not follow that everything made from them, from atoms to the entire universe, should be either self-reflexive or one of a possible reflexive pair? But therein lies a curious paradox. Imagine that in the next instant the universe switched to its mirror image. How could you tell? Would not human consciousness be reflexive also? (Whatever that means!)
Another strange case is the DNA molecule and the genetic code. Most of us are right-handed, nearly all of us have our appendix on the right, and all of us carry DNA with a right-handed twist. How are instructions for right-handedness carried genetically? Would an identical but reflected DNA molecule produce an identical but reflected organism? A lucid discussion of these and many other fascinating problems in symmetry may be found in the Ambidextrous Universe by Martin Gardner, but don't expect to find all the answers.
The half-pieces for the Eight-Piece Cube Puzzle are made from three square pyramid blocks joined together. These blocks are made from sticks of isosceles-right-triangular cross-section with two 45-degree cuts. For experimental work, the mating joints can be slightly on the loose side. A more accurate model of this puzzle made of fine woods with close-fitting joints is a delight to play with. The sharp edges may be beveled or rounded slightly to give its stark Bauhausian functionality a little more softness and warmth.
Although a well-crafted set of puzzle pieces for either of the two designs just described can be quite entertaining in itself, more important for the purpose of this book is that the geometrical principle they are both based on is even more fun to play with. It leads along an endless trail of new discoveries. For example, as suggested by Fig. 147, an obvious variation of the Six-Part Invention is to use the connection with three prongs rather than two. The three sample pieces shown in Fig. 180 assemble into a triangular cluster.
Fig. 180
By truncating the Eight-Piece Cube pieces to convert them into cuboctahedra, the puzzle remains the same but assumes an intriguing new geometry (Fig. 181).
Fig. 181
When any of the half-pieces described in this chapter are joined in threes rather than pairs, the numbers of puzzle pieces, practical sets, and possible constructions stretch the imagination. To give but one example, 12 identical pieces assemble to form the Triple Cross Puzzle shown in Fig. 182. Could you assemble 14 such pieces in axial symmetry? How about 46 such pieces?
Fig. 182
Now imagine combining all of the above into one super set containing singles, doubles, and triple pieces, and perhaps some even larger. Simply as a play construction set, who could possibly resist the urge to tinker with these pieces and fit them together different ways? At the same time, this versatile set of puzzle pieces contains practically unlimited potential as an educational tool and as a kit for discovering new puzzle problems, some of which should baffle experts. A few sample puzzle constructions are shown in Fig. 183. A large set of such pieces, well-crafted of hardwood, makes a marvelous construction set.
Fig. 183
When dissected cubes are combined with whole cubes, the number of puzzling possibilities takes another quantum jump. This idea hatched just in time for inclusion in this book, so just one simple example will be given here.
The set of seven dissimilar puzzle pieces shown in Fig. 184 could be described as three ordinary pentacube pieces and four jointed polycube half-pieces. They assemble one way only to form a 3 x 3 x 3 cube. The next time someone says that 3 x 3 x 3 cube puzzles are too easy, give them this one disassembled. Note that the half-pieces can be combined in pairs three different ways, with each pairing having four variations, so right there is ordinary puzzlement multiplied by a factor of 12!
Fig. 184
Now, if you are the type that likes to have a little extra fun sometimes, design a 3 x 3 x 3 cubic block puzzle like the above, except having only one jointed piece and with a tightly fitting joint. When carefully made these joints are practically impossible to detect. With the jointed piece assembled backwards, it looks like just an ordinary cubic block puzzle but is of course impossible to assemble.
With millions of possible combinations from which to choose, clever designs of this sort might incorporate many other interesting features such as interlocking assembly and construction of multiple symmetrical problem shapes. This leads into a whole new world of puzzling possibilities, almost totally unexplored, hence the name Pillars of Hercules. Note also that such puzzles are fairly easy to make in wood, since most of the blocks are just cubes. More intriguing still is the possibility of extending this idea to rhombic dodecahedra, with whole blocks and half-blocks combined, as suggested by the sample pieces shown in Fig. 185. Two of them form a small tetrahedron, three of them a triangle, and all five a large tetrahedron.
Fig. 185
| ©1990-2012 by Stewart T. Coffin For questions or comments regarding this site, contact the chief metagrobologist: |