[Home] [Contents][Figures] [Search] [Help]
The ways in which various geometrical solids can be packed to fill space or be assembled symmetrically in space is in itself a fascinating branch of mathematics. Being also assemblable as puzzles just makes them all the more interesting.
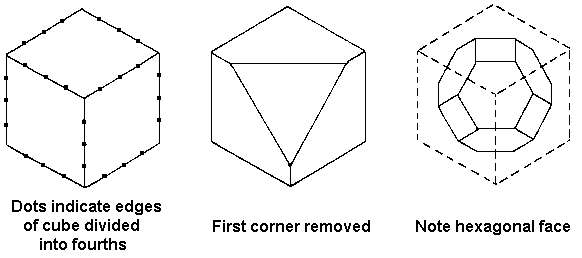
Besides the cube, there are only two other space-filling polyhedra that would appear to have much practical use as puzzle building blocks. One of these is the truncated octahedron. The blocks are fairly easy to make by starting with large wooden cubes and sawing off the eight corners using a suitable jig to hold them accurately (and safely!) in the saw (see Fig. 164). To check for accuracy, the eight new faces should be regular hexagons.
Fig. 164
There are two ways that two such blocks can be joined and six ways that three can be joined, as shown in Fig. 165. These puzzle pieces tend to be anything but interlocking, so most practical puzzle constructions using them are either pyramidal piles or are packed inside a box.
Fig. 165
The set of five pieces shown in Fig. 166 consists of two blocks joined by their square faces plus the four non-straight three-block pieces. They pack into the square box 11 different ways and make a square pyramid three different ways. Note that in the model shown the recessed bottom of the inverted box serves as a convenient base for the square pyramid. The instruction booklet that came with a commercial version of this puzzle showed 15 other symmetrical constructions using some or all of the pieces. How many can the reader discover?

Fig. 166
Puzzle pieces made up of rhombic dodecahedra joined together different ways are fascinating to play with and offer practically unlimited possibilities for geometrical puzzle constructions and mathematical analysis. The blocks are fairly easy to saw from square stock using a special jig, described in Chapter 23.
There is one way that two rhombic-dodecahedral (R-D) blocks can be joined, five ways that three can be joined, and 28 ways that four can be joined, as shown in Fig. 167.
Fig. 167
An interesting exercise is to catalog the practical geometrical constructions that might be possible using R-D blocks. All of those shown in Fig. 168 have isometric symmetry. They are arranged by increasing size, starting at the top. Those in the left-hand column have four blocks coming together at the center. Those in the middle column have six blocks coming together at the center. Those in the right-hand column have a single block in the center, and hollow versions of these are possible using one less block. Only those constructions using 20 or fewer blocks are shown. It is convenient to identify these constructions by names such as tetrahedron, even though the shape is obviously not an exact tetrahedron but only suggests it using a little imagination.
Fig. 168
At this point, one has a choice of many possible avenues of exploration. What are the fewest pieces that will construct all these shapes, or most of them, or other shapes of your choice? To put it another way, for a given number of pieces - say four or five or six - find the most versatile possible set that will construct figures. Which sets have all dissimilar non-symmetrical pieces? Which figures have unique solutions? The recreational possibilities here are practically unlimited and largely unexplored.
Polyhedral puzzles that are non-interlocking are usually more satisfactory if contained inside a box of some sort. Unlike cubes or even truncated octahedra, rhombic dodecahedra do not rest comfortably in square boxes. This can be corrected somewhat by truncating the R-D blocks. Shown in Fig. 169 is a simple but entertaining puzzle made up of 14 truncated R-D blocks joined together to make five puzzle pieces. They will construct a square pyramidal pile and also a rectangular pyramidal pile. With one piece omitted, they will construct a tetrahedral shape that, surprisingly, fits neatly inside a box. All five pieces pack neatly inside a cubic box, as shown. But the most entertaining trick they do is pack snugly into the box apparently with no vacancy, but with the single block left out!
Fig. 169
The easiest way to make truncated rhombic dodecahedra is to start with large cubic blocks and bevel all the edges at 45 degrees to any desired but uniform depth. With a shallow bevel, the mating surfaces will be small and the glue joints less strong, so it may be desirable to strengthen them by inserting dowels.
Editor's Note: This puzzle has also been called Pyracube.
Among the various ways that uniform spheres can be packed in space, they show a natural inclination to arrange themselves most densely the same way that rhombic dodecahedra pack. Thus, in the Leftover Block Puzzle or almost any other, spheres might be substituted for rhombic dodecahedra. One advantage of spheres is that they are readily available in toy stores and educational supply shops, and usually quite accurate. The disadvantage is that they are more difficult to join together strongly. They can be bonded with epoxy, but an even better way with wooden balls is to drill holes and use dowelled joints.
The substitution of spheres for rhombic dodecahedra is not exactly equivalent mathematically. Spheres have an additional symmetry that the rhombic dodecahedra lack. This is demonstrated by the mirror-image pair of R-D pieces shown in Fig. 170, both of which have the same spherical counterpart. Thus, pieces made with spheres will generally produce more solutions and construct more figures, which could be an advantage or disadvantage depending upon the circumstances. Spherical versions also tend to fall apart more easily, so the pyramidal constructions may require a retaining base.
Fig. 170
Of course, spheres might also be substituted anywhere that cubes are used. But like playing billiards with elliptical balls, one should ask not if it is possible but rather if it is practical!
Most polyhedral block puzzles are non-interlocking, including the Truncated Octahedra Puzzle and Leftover Block Puzzle previously described. All things considered, interlocking puzzles usually have more appeal. The problem here is one of complexity. For example, most practical, interlocking cubic-block puzzles require at least 64 blocks. The numbers of R-D blocks in triangular pyramidal piles are given by the following series: 4,10, 20, 35, 56, 84, ... which is the smallest of these that can be dissected into a practical interlocking puzzle? Surprisingly, the 20-block tetrahedral pile of rhombic dodecahedra can be dissected into four puzzle pieces of five blocks each that are not only interlocking but also dissimilar and non-symmetrical and assemblable in one order only. Knowing this, it is not very difficult to discover the design, so that recreation is left for the reader to enjoy. The one known design shown in Fig. 171 is believed to be unique but has not been proven so.
Fig. 171
The numbers of R-D blocks arranged in octahedral clusters are given by the following series: 6, 19, 44, 85, ... It is especially desirable that a dissection of the octahedral cluster be interlocking because it would fit so poorly into a box. There is a four-piece dissection of the 19-block octahedral cluster that is interlocking and assembles in one order only. All of the pieces are dissimilar and non-symmetrical. Three of them have five blocks and one piece has four blocks. Again, its discovery is left to the reader. The one known dissection shown in Fig. 172 may or may not be unique.
Fig. 172
The two interlocking R-D block puzzles above (Figs. 171 and 172) are both surprisingly difficult to solve. Even if the reader discovers the design by experimental dissection or some other method and makes a set of pieces, the solution has a way of vanishing from memory the moment the pieces are scrambled. Those made with spheres might be even more confusing.
| ©1990-2012 by Stewart T. Coffin For questions or comments regarding this site, contact the chief metagrobologist: |