[Home] [Contents][Figures] [Search] [Help]
Given the popularity of puzzles made up of squares joined together in different ways, it does not require too much imagination to realize that cubic blocks might be joined together in similar fashion to make three-dimensional puzzles. When measured in terms of the number of different assembly combinations possible for a given set of pieces, the cube must be the ultimate combinatorial building block. Add to that the fact that the pieces are easy to make, to visualize, to describe and to illustrate. They also pack nicely into a box or rest on a flat surface. No wonder they are so popular!
The earliest reference to 3 x 3 x 3 cubic block puzzles may be one shown in the classic Puzzles Old and New by Professor Hoffmann (Angelo Lewis), published in London in 1893, and not to be confused with the recent Botermans and Slocum book of the same name. It shows a puzzle called the Diabolical Cube, which is rather a misnomer as it is one of the easier puzzles of its type. The six pieces, illustrated in Fig. 48, assemble into a 3 x 3 x 3 cube 13 different ways. Since all of the pieces in this puzzle have reflexive symmetry, it necessarily follows that every solution must either be self-reflexive or be one of a reflexive pair. It is customary not to count these reflexive pairs as two different solutions. This particular version of what has now become a very common type of puzzle is unusual in that all of the pieces are flat and contain different numbers of cubes increasing in arithmetic progression.
Fig. 48
The next reference known to the author for the 3 x 3 x 3 cube is a version that appeared in Mathematical Snapshots, by Hugo Steinhaus published by Oxford University Press in 1950. Puzzle historians might well be puzzled by this half-century gap. With all of the interest in burrs, etc. during that time, could there have been no interest in cubic blocks? The version in the Steinhaus book (Fig. 49) has two solutions that are slight variations of each other and of medium difficulty. It is referred to as Mikusinski's Cube after its originator, the Polish mathematician J. G. Mikusinski.
Fig. 49
Nearly everyone must be familiar with Piet Hein's seven-piece Soma Cube (Fig. 50a), which is said to have been invented around 1936 and which enjoyed great popularity and commercial success around the 1960s. With 240 possible solutions, the 3 x 3 x 3 assembly is almost trivially simple. Its popularity may have been due more to the well-conceived instruction booklet showing many different problems and pastimes possible with the set. The pieces from the Soma Cube in Fig. 50b are sawn to resemble animals. It was made by Trevor Wood.
Fig. 50a
Fig. 50b
The popularity of Soma lingers to this day. Sivy Farhi publishes a booklet containing over 2000 problem figures. There have been versions with color-matching problems, with number problems on the faces and so on.
Variations on the 3 x 3 x 3 cube that have been published within the last two decades are now too numerous to mention. Commercially successful puzzles nearly always spawn a host of imitations. Even if some are well conceived or even an improvement over the original, they are almost certain to languish in obscurity, since puzzle fads tend to run in cycles with no mercy on come-lately look-alikes. But we need not be concerned with that here. As an archetype the 3 x 3 x 3 cube is a superb combinatorial puzzle - simple in principle and embodiment, yet with many secret charms still lying buried inside. Perhaps we can dig a few of them out.
With puzzles of this type, there are an optimum number of pieces; and as you tinker with them, you soon gain an intuitive sense of what that number is. There is no way that a four-piece version can be very difficult, although the one shown in Fig. 51 does have the intriguing property of being serially interlocking, meaning that it can be assembled in one order only. Is a five-piece serially interlocking version possible?
Fig. 51
The five-piece and six-piece versions of the 3 x 3 x 3 cube are the most interesting. Some of the five-piece designs are surprisingly confusing. The six-piece designs have the added advantage that they usually can be assembled into many other symmetrical problem shapes. (A very cleverly designed five-piece puzzle might have this feature too.) In order to make a systematic study of this puzzle family, the first step is to list all ways that four or five cubes can be joined (as shown in Fig. 52).
Fig. 52
The six-piece version of the 3 x 3 x 3 cube will be considered first. For aesthetic reasons, one might prefer that all the pieces be the same size, but this is impossible, so the nearest approximation is to use three four-block pieces and three five-block pieces. It is also desirable that all pieces be non-symmetrical but this is likewise impossible so two of the four-block pieces will have an axis of symmetry. All pieces will of course be dissimilar. Of the several thousand such combinations possible the author tried several that proved to have either multiple solutions or no solution, until finally finding one with a unique solution. It is shown in Fig. 53. It was produced at one time as the Half Hour Puzzle.
Fig. 53
Although it was intended to construct only the 3 x 3 x 3 cube, Hans Havermann and David Barge have discovered hundreds of other symmetrical constructions possible with this set of puzzle pieces, a few of which appear in Fig. 54. All of these figures have at least one axis or plane of symmetry, and they represent most but not all of the types of symmetry possible with this set. The cube has 13 axes and 9 planes of symmetry. Two of the figures have one axis and two planes of symmetry. Another has one axis and one plane. All the others have one plane of symmetry only. Challenge: with this set, discover a construction with one axis and four planes of symmetry - i.e. the same symmetry as a square pyramid. One is known. Are there more?
Fig. 54
In the five-piece versions of the 3 x 3 x 3 cube, there may be three five-block pieces and two six-block pieces, and none need be symmetrical. The number of such possible designs must be in the thousands, and many of them are surprisingly difficult. One is shown in Fig, 55, but readers are encouraged to experiment with original designs of their own, not necessarily using the guide-lines suggested above.
Fig. 55
Throughout this book, and throughout the world of geometrical puzzles in general it is taken for granted that the sought-for solution is not only symmetrical but usually the most symmetrical possible shape - in this case, the cube. When multiple problem shapes are considered, highest priority is given to those having the most symmetry. Evidently, one of the most basic and deeply rooted instincts of mankind is an eye for symmetry, whether in the arts, the sciences, or whatever. Trying to give reasons for so ingrained an instinct is perhaps a risky business, but here is an attempt so far as puzzles are concerned.
For reasons already explained, ideally the solution of a combinatorial puzzle, by definition, begins with the individual pieces in a state of greatest possible disorder, meaning all dissimilar and non-symmetrical. A symmetrical solution, then, goes to the opposite extreme, and does so against the natural tendency in the world toward disorder and randomness. Only the human brain is capable of doing this. Practically every human endeavor involves at least some attempt to make order out of disorder, but nowhere more graphically than in the symmetrical solution of a geometrical dissection puzzle. It is the one point to which all paths load upward and from which one call go no higher. To put it another way, the object of a well-conceived geometrical recreation is usually obvious enough so as to require minimal instructions. One tends to associate complicated instructions with unpleasant tasks - the definitive example being of course the filing of income taxes. Contrarily, life's more enjoyable pastimes tend to require no instructions at all!
Polycube pieces fit together so naturally that some persons find recreation in simply assembling random "artistic" shapes and thinking up imaginative names for them. When they don't resemble anything, the tendency is to call them "architectural designs". (Does this tell us something about the present state of architectural design, or at least the public's perception of it?)
Note that four cubes can be joined eight different ways. Packing a set of these pieces into a 4 x 4 x 2 box makes a neat but quite easy puzzle. There are said to be 1,390 possible solutions. They also pack into a 2 x 2 x 8 box, and can be split into two 2 x 2 x 4 subassemblies.
Another popular cubic block puzzle is the set of 12 solid pentominoes. Those are of course the set of pieces made by joining five squares all possible ways, discussed in Chapter 2, except in this case cubic blocks are used in place of squares. The idea of a puzzle set made of such pieces is so obvious that it probably occurred to several persons independently. The earliest references known to the author are associated with Martin Gardner's mathematical recreations column in Scientific American around 1958. They were implied in an article by Golomb in The American Mathematical Monthly, December 1954, and are discussed in his book Polyominoes.
The solid pentominoes (Fig. 56) pack into the following rectangular solids: 2 x 3 x 10, 2 x 5 x 6, and 3 x 4 x 5. Bouwkamp's computer analysis found there to be 12, 264, and 3,940 solutions to these, and these numbers have been confirmed by many other analysts. If you did not learn your lesson with the flat pentominoes, and you think that, with 3,940 solutions, packing these pieces into a 3 x 4 x 5 box ought to be easy, you are in for an even bigger surprise this time!
Fig. 56
The solid pentominoes make a very satisfactory set of puzzle pieces when accurately crafted of nice hardwoods and packaged in a suitable box. Many interesting puzzle problems and pastimes, using either the full set of pieces or subsets, are crammed into Quintillions, a booklet published by Kadon Enterprises. Or you can invent your own puzzle problems.
Fig. 57
There are 12 pentacubes that are flat (the solid pentominoes) and 17 that are not. There are 12 that have an axis of symmetry and 17 that do not. There are 12 that neither lie flat nor have an axis of symmetry. If we arbitrarily eliminate the two of these that fit inside a 2 x 2 x 2 box, then a set of 10 pieces remains (see Fig. 58).
Fig. 58
According to a computer analysis by Beeler, these pieces pack into a 5 x 5 x 2 box 19,264 different ways, and it is not very difficult to find one of them. To make this puzzle more interesting, the pieces are checkered (Fig. 59). There are two ways that one might go about this. You could randomly checker the pieces and then try to assemble checkered solutions. There are 512 different ways of checkering the pieces, of which 511 have solutions and one does not. So it would be remotely possible, if you were exceedingly unlucky, to end up that way with an impossible puzzle. The better way is to assemble the puzzle first and then add the checkering. This way you are sure of having a solution. Now try to find a second perfectly checkered solution with this set of pieces. Of the 511 ways of checkering the pieces with solutions, 510 of them have multiple solutions and one is a unique solution. So there is this very slight chance that your puzzle may not have a second checkered solution, but you may never know for sure, because finding the other solutions is very difficult (unless you use a computer). How remarkable that out of the 512 possible checkerings, just one should be impossible to assemble checkered and just one other should have a unique solution!
Editor's Note: Stewart named this puzzle Unhappy Childhood.

Fig. 59
Puzzle pieces made up of cubes joined different ways (polycubes) are of course unlimited in size and infinite in number. Those of size-six are called hexacubes, size-seven heptacubes, and so on. Questions such as how many there are of each size would more likely be pursued as curiosities in mathematical analysis rather than for practical puzzle applications. The most satisfactory polycube-type puzzles are those using small-sized pieces in seemingly simple constructions.
The interesting design possibilities for polycube-type puzzles are practically limitless. Furthermore, the pieces are among the easiest to make. For those with no access to woodworking tools, cubic wooden blocks can be obtained from educational supply stores. Also from this same source, plastic cubes that snap together are handy for experimental work.
In addition to the booklets already mentioned, World Game Review serves as a clearing house for new ideas in polycubes and related recreations.
Closely related to the polycube puzzles are the so-called packing problems using rectangular blocks. Again many of these are of interest primarily to mathematical analysts, but some of them also make satisfactory assembly puzzles. Take for example the Slothouber-Graatsma Puzzle, which calls for three 1 x 1 x 1 cubes and six 1 x 2 x 2 blocks to be packed into a 3 x 3 x 3 box. There is only one solution. Another is known as Conway's Puzzle after its inventor, mathematician John Conway. It calls for packing three 1 x 1 x 3 blocks, one 1 x 2 x 2 block, one 2 x 2 x 2 block, and thirteen 1 x 2 x 4 blocks into a 5 x 5 x 5 box. It is quite difficult unless one happens to be an expert in this particular branch of mathematics.
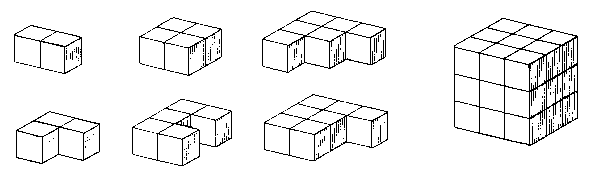
An interesting puzzle is suggested by joining 1 x 2 x 2 blocks in pairs all possible ways. The resulting 10 pieces are shown in Fig. 60. They can be assembled into a 4 x 4 x 5 solid, and there are said to be 25 solutions. Now eliminate the two pieces that are themselves rectangular, and see if the remaining eight (shaded) will assemble into a 4 x 4 x 4 cube. After you have become convinced that they will not, find a set that will by duplicating one piece and eliminating one piece, and note the interesting pattern of symmetry in the solution.
In the same vein, a simple puzzle project is to find all the ways that 1 x 1 x 2 blocks can be joined in pairs. Then assemble them into a rectangular solid and discover one solution having a pattern of reflexive symmetry
Editor's Note: Stewart named this puzzle Patio Block.

Fig. 60
| ©1990-2012 by Stewart T. Coffin For questions or comments regarding this site, contact the chief metagrobologist: |