[Home] [Contents][Figures] [Search] [Help]
Most of us have at some time in our lives enjoyed playing with those marvelous construction sets consisting of blocks with holes joined together with dowels. Many interesting variations of these are possible. In three dimensions, the simplest and most obvious are cubic blocks with holes centered on their six faces, and with dowels all the same length or perhaps in integral multiples (see Fig. 186). These are easy for the home craftsman to make. Blocks of about one-inch size can be sawn out or purchased. Quarter-inch dowels may be found in most hardware stores. The ends of the dowels are slotted with a saw and the holes are drilled slightly undersized for a tight fit. Great accuracy is not required in drilling the holes, but a spur bit and a non-grainy wood such as maple will prevent the drill from wandering.
Fig. 186
A most interesting variation is to use edge-beveled cubic blocks with 12
additional holes, as shown in Fig. 187. Many intriguing non-orthogonal geodesic
constructions can be made with a set of these. The dowel lengths will be in
multiples of ![]() .
.
Fig. 187
Another interesting variation is provided by the truncated cube (or truncated
octahedron) with its eight additional holes. These will employ dowels having
lengths in the ratio of
![]() ,
as in Fig. 188.
,
as in Fig. 188.
Fig. 188
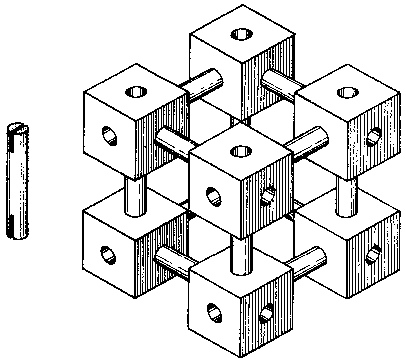
Finally, one might combine all of the above into a super-set of blocks, with all or some of the blocks having all 26 holes, together with dowels in all the appropriate lengths. One such block is shown in Fig. 189.
Fig. 189 Showing the 13 axes of cubic symmetry
Simply constructing geometrical forms with such a set of blocks and dowels can be entertaining and educational, with or without illustrations as a guide. They also have potential for puzzle problems. The seven pieces shown in Fig. 190 comprise all the ways that one block and one dowel or two blocks and two dowels can be joined, using 12-hole blocks. Can they be assembled to fit snugly into the cubic box? What other symmetrical forms will they construct?
Fig. 190
All of the sets described thus far employ radial holes - that is, with their axes all intersecting each other at the solid center of the block. There is another family of designs in which none of the hole axes intersect. The holes can be drilled straight through and the dowels can be of indefinite length. The holes will be sized for the dowels to slide freely through.
This family can be further divided into two sub-families depending upon whether the drilled components are discrete blocks or uniform sticks of indefinite length. Examples of the latter have already been shown in Chapters 6, 13, and 17.
One further variation of the Pin-Hole Puzzle is shown in Fig. 191. The square sticks have holes equally spaced and arranged alternately. The assembly of sticks and dowels forms an orthogonal lattice that can extend indefinitely in all directions.
Fig. 191
A set of such pieces might make a simple assembly plaything, perhaps to be fitted into a rectangular box. Or, with ingenuity, the idea might be developed into some sort of puzzle set. Incidentally, this entire chapter was conceived, developed, and rushed to the publisher just in time for inclusion, so many of these ideas are still "in the rough". (Are they not sometimes better that way?)
A cubic block with three mutually perpendicular non-intersecting holes drilled through it is shown in Fig. 192. It has a reflexive pair of forms.
Fig. 192
An assembly of such blocks and dowels can be extended indefinitely. In the model shown in Fig. 193 on the left, all the blocks are identical. In the one on the right, the blocks alternate right-handed and left-handed. Note the two different types of symmetry that result. Only the assembly on the right can be said to have isometric symmetry as defined in Chapter 6.
Fig. 193
Now consider the following problem: again start with a 2 x 2 x 2 assembly of cubic blocks. Again drill three holes through each block so that 12 dowels can be inserted through the pile. But this time, all eight of the drilled blocks must be identical and the assembly must have isometric symmetry. The solution is shown in Fig. 194.
Fig. 194
The three identical holes in each block are all parallel to internal diagonals of the cube, and their axes exit the faces exactly one-third the distance from both edges. To be entirely satisfactory, the holes must be drilled accurately, and this will require a suitable jig set-up plus some patience to get it adjusted properly.
This is likewise an omnidirectional construction capable of infinite expansion in all directions. It has many fascinating variations. The 2 x 2 x 2 grouping can in itself become a unit building block with 12 holes, or it could be broken into rectangular sub-units, as shown in Fig. 195.
Fig. 195
The puzzling possibilities here would appear to be practically limitless. One interesting variation uses 1 x 2 x 2 rectangular blocks. The four symmetrically arranged holes in each block pass diagonally through midpoints of sides. The blocks do not pack together but rather leave cubic and rectangular spaces. Neat symmetrical assemblies of six and twelve blocks are shown in Fig. 196.
Fig. 196
A large set of such blocks and dowels is in itself fun to tinker with, but if some of the dowels and blocks are joined permanently and assembly problems are devised around them, they become intriguing puzzles as well.
In yet another variation, shown in Fig. 197 in two different views, squat octahedra have been substituted for the rectangular blocks above. Six of these are shown assembled with 12 dowels to form a solid rhombic dodecahedron. This construction is space-filling. Note that in the view along the threefold axis, the holes are centered in equilateral triangles.
Fig. 197
Since the intriguing geometry of the rhombic dodecahedron is the basis for so many of the designs described in this book, combining it with our natural inclination for sticking pins into holes and joining things together should lead to many interesting new recreations.
By now, it should be clear that few, if any, of the designs described could be considered novel inspirations except in some small part. They all are logical offspring of previously established geometrical families, legitimate or otherwise. Mathematically speaking, the role played by the designer is often almost trivial. Once you start exploring this puzzling world of polyhedral dissections, one idea just leads to the next. Their arrangement in this work is an attempt to place the ideas in logical sequence of lineage. The problem is that one idea may have several roots branching backward in different directions. Often, one can arrive at the same place by two entirely different routes. Here is a good example:
Recall from Chapter 13 the arrangement of 12 hexagonal sticks and dowels, shown on the left in Fig. 198. Now imagine that instead of the hexagonal sticks, all of the space surrounding the dowels is filled solid. Tessellate that space into space-filling rhombic dodecahedra, and dissect the central rhombic dodecahedron into six squat octahedra, shown in Fig. 198 on the right. The result is exactly the same as the design shown in Fig. 197.
Fig. 198
The construction described above suggests compellingly by analogy dissection of other polyhedra into sections held together with dowels. Shown in Fig. 199 is a stellated rhombic dodecahedron with 12 dowels drilled through it. There are many different practical ways that this solid might be dissected, such as into 48 tetrahedral blocks, 24 rhomboid pyramids, or 12 double rhomboid pyramids, as shown.
Fig. 199
Now compare the double rhomboid pyramid above with the squat octahedron of the previous design and note that they are the same geometrical solid with the same hole locations, the only difference being in the number of holes. Thus, a set of 12 four-hole blocks and dowels constructs two rhombic dodecahedra or one stellated version. If several of the dowels are fastened in place to form lollipop pieces (Fig. 200), assembly of these figures becomes an entertaining puzzle. What is the maximum number that may be joined and still be possible to assemble?
Fig. 200
These blocks are fairly easy to saw from square stock, as explained in Chapters 8 and 9. A simple jig set-up can be used for the repetitive drilling of the holes. Since the holes are quite tilted toward the surface, a sharp spur point and soft wood are recommended to prevent wandering of the bit.
Carrying the scheme of the puzzle piece design shown in Fig. 200, to its obvious next step, make the rhombic dodecahedron itself the basic construction unit. Each block will have 12 holes. Four such blocks are shown in Fig. 201, assembled into a tetrahedral pile and pinned together by twelve dowels.
Fig. 201
In order to convert this intriguing construction set into an even more entertaining puzzle, we again join blocks and dowels to form lollipop pieces. But this time we also eliminate all extraneous holes. Not only does this save considerable drilling and improve the appearance, but it also adds greatly to the puzzling potential. By a judicious choice of hole locations, and stick locations in the lollipop pieces, simple constructions become fascinating puzzle problems. As a simple example, a triangular assembly of three blocks and three dowels is shown in Fig 202. Each block has two holes. Two pairs of blocks and dowels are joined to form lollipop pieces. The remaining dowel is the key.
Fig. 202
Note the similarities to the Pin-Hole Puzzle. The added feature of this new design is that even six or fewer rhombic dodecahedral blocks may be joined many different ways to create interesting geometrical shapes, as was shown for the Six-Part Invention in the preceding chapter. Thus, the natural appeal of pin-and-hole assembly pastimes is combined with the added feature of multiple assembly problems possible with one appropriately chosen set of puzzle pieces.
The arrangement of six blocks shown in Fig. 203 we have been calling an octahedral cluster. It uses 24 dowels. How many dowels may be attached to the blocks for it to still be assemblable? Can all the block pieces be dissimilar? What other puzzle problems can be devised using the same set of pieces? This should keep puzzle analysts busy for quite a while.
Fig. 203
There is a limit to the diameter of the dowels in relation to the blocks. The diagram in Fig. 204 shows the limit to be 1:6. In other words, if the blocks are 1½ inches across, the dowels cannot be more than ¼ inch diameter without interfering with each other.
Fig. 204
If the dowels are made slightly larger in diameter than the limit shown above, a most interesting puzzle results. Some of the dowels will require cylindrical notches milled into them. Twelve such dowels are shown in Fig. 205 assembled inside a rhombic dodecahedral block with 12 holes. Note the similarity to the 12 notched hexagonal sticks in Fig. 135a, but with some added mechanical constraints. Also, you cannot see what is going on inside. Here is a case where clear plastic might be used to advantage for the block, and perhaps even for the rods too. This puzzle scheme likewise offers recreation for the designer as well as the solver, since many different notch combinations are possible.
Fig. 205
Incidentally, the reader may have noticed the changing style of illustrations used throughout this book, alternating between photographs and pen-and-ink drawings of varying quality. The explanation is that the author was in the process of experimenting with and learning both techniques, and many of the illustrations were redone again and again right up to the publication deadline in an attempt to improve both their clarity and visual appeal. Some of the diagrams in the first two chapters were redrawn by Jack Gray using a computer and laser printer.
Most of the polyhedral illustrations started out as photographs of models, using an ancient 4 x 5 Speed Graphic camera and retouching the enlargements with pencil or pen.
Anyone who has ever tried to compile a book of this sort knows that it is, more than anything else, a learning experience for the author. The discipline of organizing the information at hand invariably leads to new ideas that must be roughed out in the workshop, analyzed, sorted and selected, with a few finished designs finding their way into the book as additions. This process of revision can become unending. Making accurate models, photographing them, developing, enlarging, and retouching is a time-consuming operation, and it tends to skew the text toward those that are easiest to fabricate, especially as publishing deadlines loom ahead. The alternative is to learn to draw one's inventions.
The graphic representation of geometrical models becomes fairly easy with practice and can be quite an interesting recreation in itself. The truth is, many of the designs shown here as pen and ink drawings, especially in the last three chapters, have never even existed as physical models as of the date of publication of this book, but rather only as abstract ideas transferred from the author's convoluted mind directly to the drawing pad. How remarkable that the human brain, given a two-dimensional graphic abstraction and a crude one at that, can in an instant mentally recreate to perfection the three-dimensional model that existed in the author's imagination - a process that might require in its physical form several days of painstaking work in a model shop by a skilled machinist or woodworker. Even more puzzling is that this bizarre geometrical re-creation should evoke so much pleasure for both the creator and the re-creator!
| ©1990-2012 by Stewart T. Coffin For questions or comments regarding this site, contact the chief metagrobologist: |