In Chapter 1, it was shown that plane dissection puzzles have much greater recreational potential when the same set of puzzle pieces assembles into many different problem shapes. The only three-dimensional puzzles described thus far having this property have been a couple of the cubic block types that form different rectangular solids and the Squirrel Cage burr set. Dissections between two different common geometrical solids present horrendous difficulties and in most cases have been proven impossible. Yet the search goes on for three-dimensional puzzles that not only assemble into different geometrical shapes but also interlock. Two designs that partially succeed are given in this chapter.
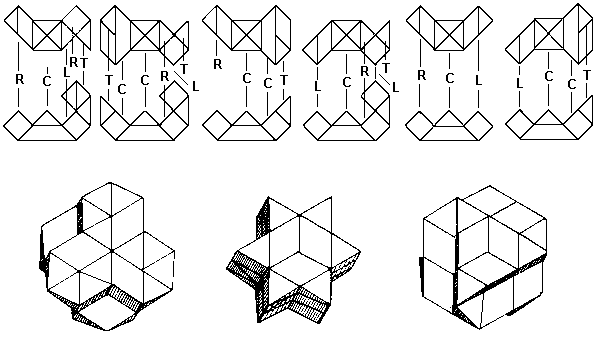
The six dissimilar and non-symmetrical pieces of the Star of David Puzzle are shown in Fig. 123a. The 27 individual blocks required in their construction are all standard building blocks from the chart in Chapter 9 and are identified by letter. This unusual puzzle assembles into three different geometrical shapes having an axis of symmetry, as well as other nondescript shapes having no apparent symmetry. All solutions have just one sliding axis of assembly. In the solution from which the puzzle derives its name, the assembly axis does not coincide with the axis of symmetry. Consequently, one blindly tries various combinations looking for the solution. Even as the correct two halves are being mated to complete the assembly, it still looks like the sort of jumble one associates with "abstract sculpture". But as they mesh together, suddenly there the solution is! This unusual and baffling puzzle presents a challenge for the skilled woodworker as well as the solver, for it is more difficult than most to fabricate well with a proper fit. The Star of David Puzzle in Fig.
Fig. 123a
Fig. 123b
The Star of David Puzzle has a relative that is mechanically much simpler but just as entertaining. This puzzle was published by the author several years ago in the form of the three axially symmetrical solutions illustrated. All the reader was asked to do was to work backwards and figure out the design of the six identical puzzle pieces. Hint: each piece is made of three standard building blocks and has reflexive symmetry. But wait - why make it so easy? The pieces are bicolored. Each of the three symmetrical solutions has two symmetrically colored forms which are almost but not quite the inverse of each other, as shown in Fig.124. Now what do the pieces look like?
Any reader who solves the above problem mentally or using pencil and paper should consider it quite an accomplishment. On the other hand, once you have the opportunity to play around with these polyhedral blocks in the flesh and experiment with fastening them together different ways, the solutions to this and other similar problems should all become perfectly obvious. Not only that, but in the process you will probably discover other interesting dissections as well.
Fig 124d
