[Home] [Contents][Figures] [Search] [Help]
In the previous chapter, simple totally symmetrical dissections were transformed into puzzling problems through the use of coloring. We will now explore the combinatorial complexities created by making the pieces dissimilar in shape.
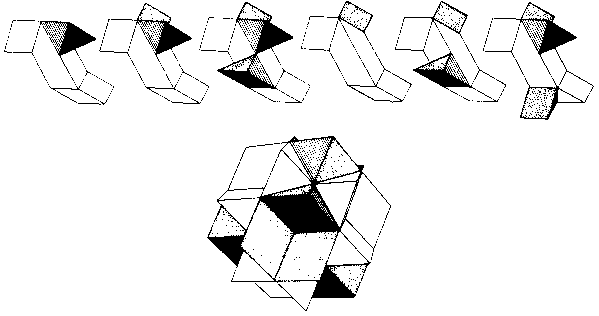
As already explained in Chapter 8, the second stellation shape is obtained by adding twelve rhombic pyramid blocks to the Four Corners Puzzle. As each block is added, there is a choice of two surfaces to which it can be attached. The six puzzle pieces shown in Fig. 108 represent all of the non-symmetrical ways of attaching such blocks. The added blocks are shown shaded. By an amazing coincidence, this just happens to use the required twelve blocks and yield the required six puzzle pieces. This quite satisfactory combinatorial puzzle has two solutions of moderate difficulty.
Fig. 108
The fortuitous geometrical circumstance occurring with the Permutated Second Stellation, which allows the second stellation to be assembled from a fully permutated set of puzzle pieces, can be exploited in many other polyhedral shapes. The analogous set of pieces for the third stellation is shown in Fig. 109. It likewise has two solutions and four sliding axes. Theoretically, it should be no more difficult than the second stellation, but it is probably slightly more confusing because of the greater irregularity of the pieces.
Fig. 109
Carrying the development of the Permutated Second Stellation and the Permutated Third Stellation one step further, by lengthening the triangular stick segments even more, one arrives back at an assembly that resembles the nest of twelve triangular sticks shown in Fig. 93, except that now some of them are broken in two internally. The six dissimilar puzzle pieces are shown in Fig. 110. Because of the extra length of the arms, they now interfere with each other during assembly. By an extraordinary coincidence, this results in one of the two solutions being impossible to assemble and three of the four sliding axes being blocked. Thus the puzzle has only one solution and one possible sliding axis of assembly. Consequently it is very difficult.
This remarkable puzzle design has been described as though it were a coincidence of four coincidences. But is it really? The term coincidence would seem to imply chance or luck, whereas this is simply a mathematical reality of the way things are in this world. The only luck involved was that of the person discovering it. Or was it? Perhaps the universe itself is the ultimate example of an improbable coincidence. Why are things as they are?
With the addition of yet 12 more rhombic pyramid blocks to the permutated second stellation of the rhombic dodecahedron, it is transformed into the intriguing polyhedron shown in Fig. 111, which is an intermediate form between the second and third stellations. More importantly, these added blocks have the same practical effect as did the lengthening of the arms in the Broken Sticks Puzzle. That is, one of the two solutions is eliminated and three of the four sliding axes are blocked. Besides forming an attractive polyhedral sculpture with simple clean lines, especially when made of contrasting exotic woods, its snugly interfitting pieces do not require much dexterity to assemble. All things considered, this is a most satisfactory puzzle.
In this and the previous two chapters, various polyhedral blocks derived from dissections of the rhombic dodecahedron have been employed for building up puzzle pieces. If the geometry of these pieces is not entirely clear to the reader from the drawings alone, some hands-on experience with the blocks should help to clarify things. If the requirement for accuracy is set aside for the moment, they are all easy to make even with hand tools. This is a good point at which to summarize them.
For our purposes, the tetrahedral block is taken as the most basic unit, although of course it could be further subdivided ad infinitum. Since many of the blocks are made equally well from either square or triangular stock, this is conveyed with two sets of drawings in Fig. 112.
| Triangular Stock | Square Stock | ||
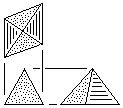
| T | Tetrahedral Block Basic unit. Made from triangular stock without waste or square stock with waste. See Fig. 90 for more information. |
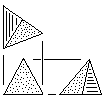 |
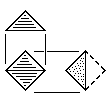 |
| P | Rhombic Pyramid Block Two tetrahedral units. Made from triangular stock without waste or square stock with waste. |
 |
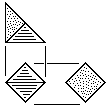 |
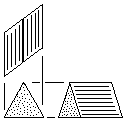
| R | Right-Handed Prism Block Three tetrahedral units. Made from either triangular or square stock without waste. |
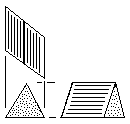 |
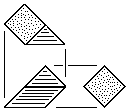 |
| L | Left-Handed Prism Block Three tetrahedral units. Made from either triangular or square stock without waste. |
 |
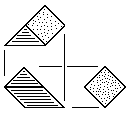 |
| O | Squat Octahedron Block Four tetrahedral units. Made from square stock with waste. Also made of two rhombic pyramid blocks. |
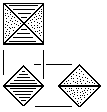 |
|
| C | Six-Sided Center Block Six tetrahedral units. Made from square stock without waste. Also made of two prism blocks. See Fig. 90 for more information. |
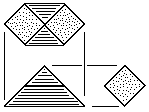 |
|
Fig. 112
For further clarification, Fig. 113 shows rhombic dodecahedra dissected into these various shapes. The rhombic dodecahedron itself is used as a basic building block in Chapter 8.
Fig. 113
With only these six building blocks, the number of simple ways in which they can be combined into interlocking puzzles is phenomenal. Just a few more examples will be shown in this chapter.
The single puzzle piece shown in Fig. 114 consists of a six-sided center block to which have been attached two right-handed prism blocks. Six such identical pieces assemble into an interlocking configuration as shown, with three gaps in each of the four corners. These gaps are filled with 12 rhombic pyramid blocks. Each block can be attached to either of two adjacent pieces. There is one and only one way of attaching them whereby six dissimilar nonsymmetrical puzzle pieces are created, as shown. They assemble one way only, with only one sliding axis, to make a very satisfactory puzzle. The appearance of the puzzle is enhanced by using a contrasting wood for the added blocks.
Often two polyhedral dissections may be internally similar and functionally identical as assembly puzzles, even though their external appearances are quite dissimilar. Here is a good example.
The single puzzle piece shown in Fig. 115 consists of three six-sided center blocks joined together. Six such identical pieces assemble into an interlocking configuration as shown, with three gaps in each of the eight corners. These gaps are filled with 24 rhombic pyramid blocks attached in such a fashion that six dissimilar non-symmetrical puzzle pieces are created. The six sides of the assembled puzzle are then truncated into square faces, making it cubic. The sliding axis for the first step of disassembly is an internal diagonal of the cube and can be rather tricky to locate. Thus, this puzzle is entertaining both to solve and to disassemble. It is also quite attractive in two contrasting woods, with the six faces sanded and polished.
If the Diagonal Cube Puzzle is incidentally tricky to disassemble, this theme is carried one step further in the next example, which is made deliberately so.
Each puzzle piece consists of a six-sided center block, to each end of which is attached another six-sided center block and a prism block. In the version shown in Fig. 116, a right-handed prism block is at one end and a left-handed one at the other end, so that each piece has reflexive symmetry and all six pieces are identical. (Other more complicated versions are possible having dissimilar pieces.) The puzzle is assembled with no great difficulty by mating two mirror-image halves to form an interesting polyhedral shape having the appearance of a cluster of six rhombic dodecahedra. To disassemble it, however, three fingers of each hand must be placed in exactly the correct places and pushed in opposition to start the two halves apart along their one sliding axis. Even when made slightly loose so that it rattles in one's hands, random poking and prying will seldom dislodge the two halves. A truncated version is also shown.
| ©1990-2012 by Stewart T. Coffin For questions or comments regarding this site, contact the chief metagrobologist: |