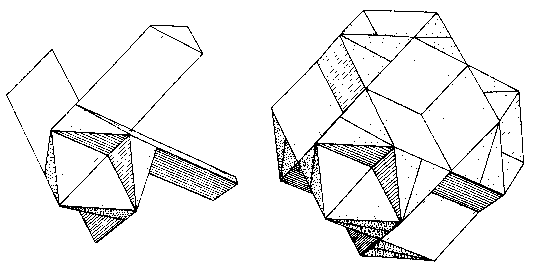
Referring back once again to the now familiar cluster of 12 triangular sticks in Fig. 93, divide each stick in two longitudinally. This produces a totally symmetrical arrangement of 24 sticks of 30-60-90-degree triangular cross-section. These sticks are then joined in fours to make a simple but intriguing geometrical puzzle. In the model shown in Fig. 137, the ends of the sticks have been cut off at an angle, giving the assembled puzzle the envelope of a rhombic dodecahedron with eight hexagonal dimples and six square dimples.
Fig. 137
When accurately made, this puzzle feels solid when handled, and it may take a while to discover that it can be slid apart along any one of its four sliding axes into two identical halves. The puzzle is assembled by the reverse of this with no great difficulty. However, the assembly sometimes has a surprise ending. For some reason, many persons feel the urge to toss this puzzle into the air after they have assembled it. Perhaps it is because it is more nearly spherical than most and feels so solid. The theory of interlock indicates this to be truly an interlocking configuration, but it fails to take into account that the pieces all rotate slightly and free themselves from one another. The usual result is that it flies apart in all directions!
This puzzle lends itself very well to multicolor problems. Four contrasting colors are used for the 24 sticks, six of each color. The six puzzle pieces are made up of all possible permutations of the four colors. There are four solutions having color symmetry. In the first and most obvious, like colors are mated in pairs and all like colors are mutually parallel. In the second, like colors are again mated in pairs but form four rings around the outside. In the third, all hexagonal dimples are solid colors. In the fourth, no like colors touch each other. The black and white representations of these are shown in Fig. 138. Discover a simple transformation from one to another.
Fig. 138
This puzzle was produced at one time under the name of Scorpius. Since the configuration is very useful and leads to many other interesting designs, rather than refer back to it by some complicated yet ambiguous geometrical description, it will be more convenient simply to call it the Scorpius configuration.
One interesting variation of the Scorpius Puzzle has six puzzle pieces that are identical but non-symmetrical. As shown in Fig. 139, this is accomplished by starting with the symmetrical Scorpius piece and exchanging one arm with its mating half, hence the name. This puzzle has two distinctly different mechanical solutions. If four different colors are used for the arms, there is one way of coloring them such that the two different mechanical solutions produce two different symmetrical coloring patterns, corresponding to the first two shown for the Scorpius Puzzle.
Fig. 139
The 24 sticks in the Scorpius configuration lend themselves naturally to being joined in fours in different ways to create a combinatorial puzzle. Not counting side-by-side pairs, there are 10 different ways of joining four such sticks. Of these, one is symmetrical, two are impossible to assemble, and one does not permit any solutions. By a most extraordinary stroke of luck, the remaining six pieces, shown in Fig. 140a, assemble one way only with only one sliding axis and in essentially only one possible order to create a combinatorial puzzle of intriguing geometry and considerable difficulty. The Scrambled Scorpius in Fig. 140b was made by Mark McCallum.
Fig. 140a
Fig. 140b
