All of the burr puzzles described in the previous chapters have been orthogonal, i.e. rectilinear, Cartesian, with right angles. They are the most familiar and the easiest to visualize, analyze, explain, and make (but not necessarily to solve!). The time has now come to venture beyond the comfortable world of right angles and explore the wondrous geometry of the diagonal burr.
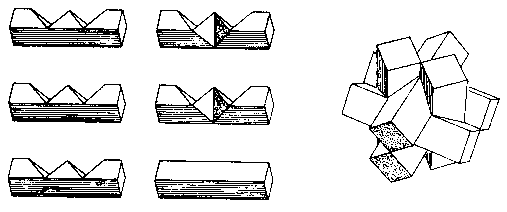
The diagonal burr can be regarded as a standard six-piece burr in which all of the sticks have been rotated 45 degrees, with the notches V-shaped rather than square. The six pieces shown in Fig. 85 represent one version. The piece with no notches is of course the 'key" which slides in last to complete the assembly. Two of the other pieces have an extra notch to accommodate it. The reader can probably solve the puzzle mentally by studying the drawings. It is also easy to whittle a rough model from square sticks of some soft wood.
Fig. 85
After having solved this puzzle one way or the other, now make the surprising discovery that the "key" is not really a key piece at all, but more properly called a pseudo-key. It need not go in last or come out first. In fact, it need not even be used. The burr can be assembled in total symmetry using six identical pieces with two notches each by mating two mirror-image halves of three pieces each (Fig. 86).
Fig. 86
Like its orthogonal counterpart, the origin of the diagonal burr is a mystery. The earliest US Patent is No. 393,816 to Chandler in 1888, but it shows a more complicated version with sliding key. The earliest record of the symmetrical version appears to be US Patent No. 779,121 to Ford in 1905. Curiously, in his patent description, Ford shows a very awkward method of assembly rather than the simple mating of two halves.
The diagonal burr has also had its share of variations over the years. As you might expect, a favorite theme of puzzle inventors has been to increase the number of pieces, which is quite easy to do with this type of arrangement. Carrying this to the extreme, US Patent No.774,197 to Pinnell in 1904 (Fig. 87) shows a horrendously complicated assembly of 102 diagonally notched sticks. (The patent notes that no model was submitted!) Another variation has been to enclose the burr in a spherical outer shell (US Patent No. 766,444 to Hoy in 1904 and US Patent No. 1,546,025 to Reichenbach in 1925).
Fig. 87
Someone, somewhere, perhaps in the mid-19th century, made the marvelous discovery that the ends of the diagonal burr sticks can be beveled to produce a puzzle that, when assembled, is the first stellation of the rhombic dodecahedron. According to puzzle collector and historian Jerry Slocum, a puzzle of this sort was sold as early as 1875. The only patent on it that the author is aware of is Swiss Patent No.245,402 to Iffland in 1946.
The word intriguing is used frequently throughout this book to describe various polyhedral dissections, but none can outshine the brilliance of this simple dissection (Fig. 88). From one point of view, it may be regarded as a diagonal burr puzzle in which beveling the ends of the pieces produces a totally unexpected and beautiful new shape. From another point of view, it is a surprising dissection of the stellated rhombic dodecahedron into six identical pieces that amazingly assemble and interlock! It has more interesting properties too: when viewed along one of its fourfold axes of symmetry it is square, while along one of its threefold axes it is the Star of David. And perhaps most surprising of all, it is a space-filling solid.
Fig. 88
Although a rough model of the diagonal burr is easily whittled from soft wood or sawn by hand, to be entirely satisfactory it should be made very accurately, for which power tools and jigs are required. It is also quite susceptible to changes in humidity when made in wood, so stable woods should be used. It is often manufactured in plastic, which overcomes this problem.
The solution to the diagonal burr is so easy as to be barely a puzzle, but the stellated version does require some dexterity and patience, especially when accurately made with a tight fit. A problem with the stellated version in wood is that the sharp ends of the pieces are across the grain and easily broken. This can be corrected by making each piece of three blocks glued together. Although woodworking techniques are discussed later, a method for making these blocks will be explained briefly here as an aid to understanding their geometry. This will be easiest if the reader can actually saw some out, but perhaps others can imagine doing it.
As shown in the drawing in Fig. 89, each puzzle piece consists of a six-sided center block to which are attached a pair of tetrahedral end blocks. The six-sided center blocks are easily made as follows: start with uniform square sticks of any convenient size - say one-inch square. Make a V-shaped cradle (Fig. 90) that holds the sticks at a 45-degree angle of rotation and slides in the miter grooves of a table saw at an angle of 45 degrees when viewed from above. Make a diagonal cut on the end of the stick. Then rotate the stick 180 degrees and advance it in the cradle exactly the correct amount to produce a pyramidal point in the center when the second saw cut is made. Continue in this manner to make additional blocks without waste. This very useful building block will be used frequently in the chapters that follow and will be referred to as the six-sided center block.
Fig. 89
Fig. 90
The two end blocks are made using the same square stock in the same cradle, except that the stock is advanced a shorter distance when making the second cut, and there will be a piece of waste for each one made. These are referred to as tetrahedral blocks. They are not regular tetrahedra - two opposite dihedral angles are right angles and the others are 60 degrees. These are also useful building blocks, both practically and mathematically. Many of the geometrical shapes to be discussed in the next three chapters can be regarded as made up of these blocks. For example, the six-sided center block contains six of these units, the whole piece therefore eight, and the entire puzzle 48. The rhombic dodecahedron is made up of 24 of them, with each stellation containing two additional units.
