| 1 | Introduction |
| 2 | An Elegant Six-Block Cycle |
| 3 | Construction of the Cube |
| 4. | The Origins of the Cube |
| 5 | Conclusions |
| 6 | References |
There are many cases where a gem of an idea has lain buried in the library for years, only to be uncovered and resurrected later. O'Beirne's Cube is one of these. This is a box-packing problem described by T. H. O'Beirne in his "Puzzles and Paradoxes" column in the British magazine, The New Scientist, over 35 years ago [1] . This is a splendid puzzle but did not appear in O'Beirne's 1965 book [2], nor has it appeared in the more popular puzzle compendia since then, [3], [4]. It does appear in a more recent book [5] but the description is cryptic at best. Most puzzlers aren't aware of it but they should be. This article is an attempt to bring this cube to public attention and to explore the processes that lead to O'Beirne's discovery.
The cube that O'Beirne describes is a classic box-packing problem. There are six pieces, quite irregularly shaped, which can be packed into a cube or five other rectangular solids. In this respect, it is similar to Piet Hein's Soma [6], seven pieces that fill a 3 x 3 x 3 cube, or Solomon Golomb's Pentominoes [7], a set of planar figures that fill a 3 x 4 x 5 box, among others, if made one unit thick. These latter two puzzles are probably the best known box-packing puzzles -- due to their versatility and to their commercial success -- but are by no means the only ones. Steinhaus [8], for example, describes a set of six irregular pieces which, like Soma, fit together as a 3 x 3 x 3 cube but which, unlike Soma, do so in only two ways. Van Delft and Botermans [3] describe some additional intriguing box-packing problems by John Conway and Jennifer Haselgrove.
O'Beirne's Cube is a box-packing puzzle at one level but a brick-packing puzzle at another. Brick-packing [9] is a sub-genre of box-packing in which all the pieces must be regular rectangular solids, or "bricks". O'Beirne's Cube consists of six movable and irregular pieces but each of these pieces, in turn, consist of four 6 x 4 x 3 bricks which do not move relative to each other. Hence, the problem can also be defined in terms of packing 24 bricks into the specified boxes.
A box-packing puzzle, in one sense, is easy to construct: Take a rectangular solid of whatever dimensions and saw through it repeatedly producing a number of smaller irregular pieces. If too many pieces are produced, the puzzle is trivial; in the extreme case, we could reduce a block to sawdust and guarantee it would fit almost any shape. A box-packing puzzle becomes important when it uses the minimum number of pieces to produce a desired effect. O'Beirne's Cube is more meaningful in terms of the six irregular pieces rather than the more numerous bricks.
To be truly interesting, a box-packing puzzle requires a further quality, elegance. This may seem subjective but is not unknown in science. H. E. Dudeney [10] considered it essential for all "puzzle crazes" and Hofstadter [11] waxed eloquently on the "primordial appeal" of Rubik's Cube and its variations. Elegance is what Roger Penrose [12] meant when he referred to some scientific theories as "beautiful" theories. A box-packing problem becomes interesting when it shows us a relationship among elements that we didn't perceive or expect and becomes truly elegant if we're impressed by this new information. Soma achieves this status by showing us a new theorem, that is, that all the irregular shapes, i.e., non-brick shapes, produced by joining four or fewer cubes can be assembled into a larger cube . With pentominoes, it's the realization that the twelve shapes produced by joining together five square tiles in all possible planar combinations, without rotation or reflection, will cover a 6 x 10 rectangle.
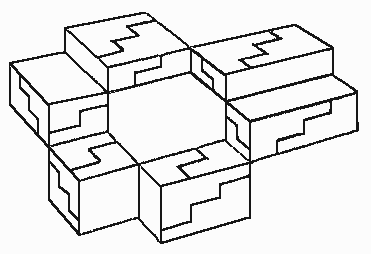
The six shapes devised by O'Beirne fit together as a 12 x 12 x 12 cube. The cube can then be broken stepwise on one plane and reassembled as a 12 x 8 x 18 brick or it can be broken on a second plane and reassembled as a 12 x 9 x 16 brick. Any arrangement of the pieces into a rectangular solid always guarantees that it can be dissected stepwise on two planes and rearranged into either of two new shapes. This produces the cycle of six shapes which are shown in Figure 1. The idea of a stepwise dissection was mentioned in 1893 by Hoffman [13] and has been a standard device with puzzlers such as H. E. Dudeney [14]. The principle is normally applied to a two-dimensional figure so that a rectangle, such the one in Figure 2, could be divided into two columns and three rows, cut stepwise on the diagonal, then rearranged into three columns and two rows. The only requirement is that the number of rows, n, exceed the number of columns, n-1, by one or vice-versa.
.
Figure 1: The cycle of the six blocks (adapted from the New Scientist).
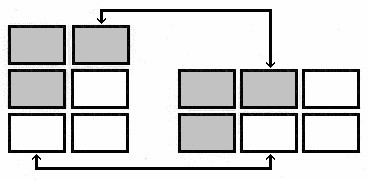
Figure 2: The stepwise dissection of one figure produces another; note the ratio of the sides.
The stepwise dissection is an old trick on a plane surface but O'Beirne showed that it could be applied at the same time to two surfaces of a cube. The slippage from one shape to another and the cyclic nature of the series is both charming and aesthetically pleasing, that is, truly elegant.
But there is a second source of elegance in the puzzle. The six large pieces are based on 24 bricks. There are exactly three ways to combine two of these into a larger brick. Pairs of the 24 small bricks are combined into 12 mid-sized bricks with four of every possible combination. These 12 mid-sized bricks are then combined, by joining them at right angles using every possible combination, to produce the six, larger irregular pieces. The large pieces then form two sets with each set containing pieces that are mirror-images of the pieces in the other set. To form a cube, each piece is placed in a position which is diagonally opposite the piece which is its mirror-image complement.
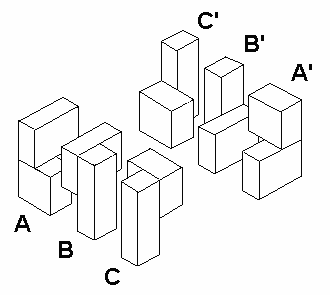
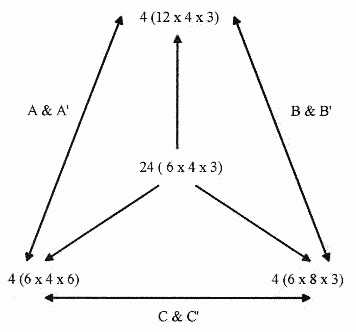
The pieces of the puzzle and their arrangement are shown in Figure 3. Each of the six pieces has the same volume because each is built of four 6 x 4 x 3 bricks. Within each piece, the four small bricks are arranged as two sets of two, each forming two larger bricks. If we consider all the possible ways that two 6 x 4 x 3 bricks can be joined to form a larger brick, there are only three, corresponding to joints on the ends, the top, or the front. Thus, two 6 x 4 x 3 bricks can form a new brick that is twice as long, twice as high, or twice as deep. This is shown in Figure 4. The three sets of mid-sized bricks are then used to build the six irregular shapes which are labeled A, A', B, B', C, C'. The prime indicates a complement to the corresponding piece. The irregular pieces are formed by joining each possible pair of mid-sized bricks transversely at the ends of their longest axes. The labeled pieces in Figure 3 correspond to the labeled pieces in Figure 4.
 |
 |
|
Figure 3: An isometric projection of the
assembly |
Figure 4: The construction of the six pieces. |
When the pieces are assembled, as shown in Figure 3, they can then be separated stepwise and reassembled in the shapes shown in Figure 1. The step cycle works, if and only if, the surface to be dissected can be divided into n rows and n-1 columns or vice-versa. At any point in the cycle, the current brick shape yields the equivalent of 2, 3, and 4 units, respectively, on the three axes. Thus, there are always two new bricks that can be produced from the current state based on the 2,3 or 3,4 dissections but not a third because the 2,4 split is incompatible with the stepwise move.
The overall effect is quite intriguing. Most people intuitively grasp the idea of the stepwise cut and are not surprised by a transformation in one direction. A similar in another dimension is unexpected and this piques the interest of most people. They are then captivated by the cyclical nature of the transformations and enjoy shifting the blocks from one shape to another. (There are those who are impervious to the charms of the device but they probably wouldn't read this journal!)
O'Beirne's Cube is amazing and delightful. While it may not rank with the discovery of pentominoes or Rubik's Cube, it is a good example of mathematical creativity and discovery. When we first experience the six-block cycle we are struck by "How did he think of it?", that is, what train of thought, what psychological processes, lead to such a discovery? If we assume that good ideas do not emerge fully formed from nothingness, we ought to be able to trace the ideas that lead to O'Beirne's discovery.
The process we see with O'Beirne fits what Douglas Hofstadter [15] has called the "crux of creativity". Hofstadter offers his views on creativity after two columns in the Scientific American in which he discusses Rubik's Cube [16] and the wondrous variety of three-dimensional sliding puzzles that followed [11]. The issue, for Hofstadter, is whether the variations on the original cube are creative in their own right. Hofstadter not only answers in the affirmative but concludes that: "Making variations on a theme is really the crux of creativity [author's italics] [15, p. 233]. True to the AI tradition, Hofstadter argues that thought is not random but follows a progression as one state is transformed to another. If we retain the given rules and elements, we can mentally explore what Newell and Simon [16] defined as the "problem-space", that is, the tree-structure of permutations and combinations available within the defined domain; if, however, we alter the rules or the elements, we begin to define a new problem-space. Hofstadter [15, p.237] refers to "slippage" as we explore the possibilities, quite unconsciously, of changing one parameter or another beyond the previously defined limits. Hofstadter argues that the changes will not be random but will be based on "reminding-incidents" as the current state evokes previously stored knowledge and this knowledge becomes the foundation for further change. Margaret Boden [18, p. 113-123], another AI advocate, describes a similar process she refers to as 'relaxation of structural constraints' and insists that it must be coupled with an evaluative assessment that recognizes when an interesting new product has been produced.
If Hofstadter and Boden are correct, we should be able to identify (1) one or more simple themes that O'Beirne was pursuing, (2) one or more reminding incidents that evoke previous knowledge, and (3) an emerging pattern that could be recognized as interesting by a skilled expert.
In O'Beirne's case, we can see all three elements. First, we have to begin with the assumption that O'Beirne was aware of the stepwise dissection of a rectangle. Almost certainly he must have been; this is too old a trick to be missed by someone writing a puzzle column. Second, we can assume that O'Beirne did not begin by looking for a block with these queer properties but, rather, became aware -- probably quite suddenly -- that one could be produced.
We get a hint of O'Beirne's train of thought by examining his previous column in The New Scientist [19]. His columns appeared weekly so it seems likely that the train of thought in one column would directly influence the next. In this preceding column, O'Beirne poses two relatively simple problems for his readers. Both are designed to get the readers to use factoring to solve a brick-packing problem.
The first problem begins with the observation that five saw cuts on one side will divide a 6 x 6 x 6 cube into six 1 x 6 x 6 bricks. These smaller bricks can then be packed together to form five and only five larger bricks, including the original 6 x 6 x 6 cube. The reader is asked to discover the five larger bricks and to prove why these are the only ones possible. The solution, of course, is to realize that the gross volume of the large brick must always be 216 units and that this must be factored into three elements, two of which must be divisible by 6. The five bricks can be considered a linear sequence as shown in Figure 5.
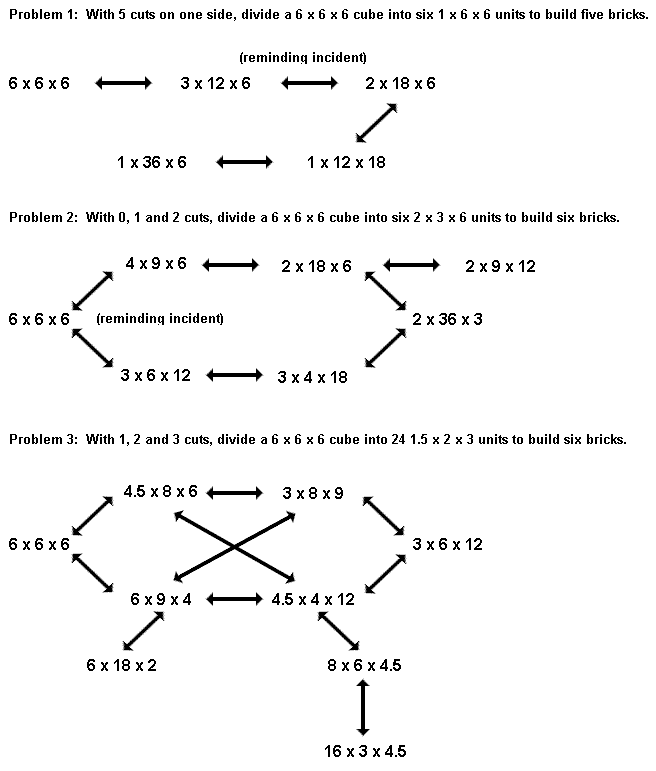
Figure 5: The three problems that O'Beirne posed. Note that I have rephrased the third.
Within the sequence of bricks for problem 1, there is a combination that includes the stepwise dissection. The change from a 3 x 12 x 6 to a 2 x 18 x 6 brick must be a "reminding incident" for the stepwise cut.
The second problem follows the logic of the first. The theme, again, is saw cuts on a cube but the "slippage" involves using two surfaces rather than one. Three saw cuts can reduce a 6 x 6 x 6 cube to six 2 x 3 x 6 bricks, if we stack the pieces for the second or third cuts so that we have one cut on one surface and two on another, and, by default, zero on the third surface. These bricks can be stacked in seven and only seven ways to produce a larger brick. Again, the trick is to factor an expression that yields a volume of 216 with three elements, each of which must be divisible by 2 or 3 or both.
The sequence of transformations for problem 2, as shown in Figure 5, contain two aspects that are important. First, there are two transformations that again involve the stepwise dissection and would further "remind" O'Beirne of this old trick. Second, there is a cyclic pattern that emerges with the transformations from brick to brick. O'Beirne would certainly recognize this as an intuitively interesting pattern.
After posing the second problem, O'Beirne [19, p. 493] then leaves the reader to ponder a third problem
Our problem for next week is to find a set of equal-volume pieces which can be packed to fill any one of six [author's italics] different rectangular-block shapes only, one of which is a cube.
The answer to this problem is the set of pieces described in Figure 3.
The reader is asked to begin the third problem with the goal as defined but it seems unlikely that O'Beirne started at this point. Rather, it seems likely that he thought of it as an extension of problem 2. Problem 2 uses 0, 1, and 2 cuts to produce a cycle which includes two stepwise dissections using a 3:2 ratio and all other dissections use a 2:1 ratio. If we follow the theme to use 1, 2, and 3 cuts per side, we get 24 units which produce a cycle of six transformations using stepwise dissections of either 4:3 or 3:2 ratios. The 24 units, of course, are an inelegant number and will produce more bricks than the six shown in Figure 1. All that O'Beirne had to do -- and this is testimony to his ingenuity -- was to realize that the problem could be simplified by "freezing" some pieces in position so that only the cycle of stepwise transformations could be produced. This eliminates the inelegant combinations, some of which are shown in Figure 5.
O'Beirne's six-cycle stepwise cube is a marvelously elegant box-packing puzzle. It would appear that O'Beirne discovered this puzzle while posing some simpler brick-packing problems for his readers. This first problem involved cuts on only one side of a cube but did include one transformation using a stepwise dissection, an old trick that he would have immediately recognized. The second problem extended the cuts to two sides and, unlike the first, yielded a cycle of six transformations, two of which used the stepwise dissection. O'Beirne appears to have followed this theme by considering cuts on three sides which yielded a cycle of stepwise transformations. Holding some of the small bricks in position reduced the number of pieces to six irregular shapes and limited the combinations to the six in the cycle.
While we can recapitulate the train of thought that lead to this discovery, we must not assume that just anyone following the same path would have made the same discovery. O'Beirne could capitalize on these events because he was able to recognize an intuitively interesting and elegant combination of pieces. Ultimately this discovery hinged as much on aesthetic judgement as it did on mathematical knowledge but that may be true of all great discoveries.
[1] T. H. O'Beirne (1961). Puzzles and paradoxes:#9; A six-block cycle for six step-cut pieces. The New Scientist, #224, 560-561.
[2] T. H. O'Beirne (1965) Puzzles and Paradoxes. New York: Oxford University Press.
[3] P. van Delft and J. Botermans (1979). Creative Puzzles of the World. New York: Harry N. Abrams, Inc.
[4] J. Slocum & J. Botermans (1986). Puzzles Old and New. Seattle, WA: University of Washington Press.
[5} J. Slocum & J. Botermans (1994). The Book of Ingenious and Diabolical Puzzles. New York: Random House.
[6] Martin Gardner (1961). The Soma Cube, in More Mathematical Puzzles and Diversions. Hamondsworth, U.K. : Penguin.
[7] Solomon Golomb (1965). Polyominoes. New York: Scribner.
[8] H. Steinhaus (1969). Mathematical Snapshots. New York: Oxford University Press.
[9] D. A. Klarner (1973). Brick-packing puzzles, Journal of Recreational Mathematics, 6, 112-117.
[10] H. E. Dudeney (1926). The psychology of puzzles crazes, The Nineteenth Century Magazine, 100, 868-879.
[11] D. R. Hofstadter (1985). On crossing the rubicon, in D. R. Hofstadter (ed), Metamagical Themas: Questing for the essence of mind and pattern. New York: Bantam. p. 329-363. (original in Scientific American, July, 1982).
[12] R. Penrose (1989). The Emperor's New Mind. New York: Oxford University Press.
[13] Professor Hoffman (1893). Puzzles Old & New. New York: Frederick Warne & Co.
[14] H. E. Dudeney (1917). Amusements in Mathematics. Reprinted 1958, New York: Dover.
[15] D. R. Hofstadter (1985) Variations of a theme as the crux of creativity, in D. R. Hofstadter (ed), Metamagical Themas: Questing for the essence of mind and pattern. New York: Bantam. p. 329-363. (original in Scientific American, October, 1982).
[16] D. R. Hofstadter (1985) Magic cubology, in D. R. Hofstadter (ed), Metamagical Themas: Questing for the essence of mind and pattern. New York: Bantam. p. 329-363. (original in Scientific American, March, 1981).
[17] A. Newell & H. Simon (1972). Human Problem-Solving. Englewood Cliffs, NJ: Prentice-Hall.
[18] M. A. Boden (1989). Artificial Intelligence in Psychology: Interdisciplinary essays. Cambridge, MA: M.I.T. Press.
[19] T. H. O'Beirne (1961). Puzzles and paradoxes: #8; Golden section and the Wythoff series. New Scientist, 3223, 492-493.